Poder coletor, poder resolvente e fator de ampliação estão na base da pequena luneta de Galileu e permanecem como referências mesmo para telescópios modernos.

Para comemorar os 400 anos da invenção da luneta por Galileu Galilei, a União Astronômica Internacional (IAU, em inglês), em parceria com a ONU e a Unesco, definiu 2009 como o Ano Internacional da Astronomia.

Para uma abordagem histórica do telescópio certamente vale a pena começar com a consideração de que o olho humano é um órgão tão fantástico que milhares de anos se passaram antes que pudéssemos perceber que ele tem limites e que esses limites podem ser superados. O telescópio foi o primeiro instrumento usado para tornar visíveis coisas antes invisíveis.

Ao longo de quatro séculos essa extensão do olho se expandiu em muitas direções: tamanho, acuidade, faixa espectral, rapidez de resposta e tempo de acumulação de luz. Hoje ela opera em separado do corpo, de modo robótico, transmitindo imagens a distâncias de bilhões de quilômetros. Para compreender o funcionamento de um telescópio é preciso conhecer seu princípio, dado por Galileu. Deixando uma série de detalhes (técnicos e históricos) de lado, vamos nos concentrar nos três parâmetros que propiciaram essa revolução: poder coletor, poder resolvente e fator de ampliação.

A luz da maioria dos astros é tão fraca que é preciso coletar mais que a capacidade do olho para enxergá-los. Para isso, usa-se uma lente (também chamada de objetiva), que obviamente tem de ser maior que a pupila na entrada no olho. O poder coletor é simplesmente o número de vezes que a área da objetiva é maior que a pupila. (Lembre-se de que a área de uma figura circular é proporcional ao quadrado do diâmetro.)

Uma pessoa de visão média, olhando para o alto do céu numa noite límpida, sem a presença da Lua ou de luzes artificiais, enxerga estrelas de até magnitude 6. Isso equivale a enxergar a sétima estrela do aglomerado das Plêiades. Por isso, no interior do Brasil, esse asterismo é chamado de “setestrelo”. Galileu não tinha uma visão particularmente boa, pois a olho nu só enxergava seis das sete estrelas desenhadas em claro e negrito. As demais, representadas por pontos, ele só observou porque a objetiva da luneta tinha um poder coletor maior que o de sua pupila. Quanto teria sido esse fator?

Não sabemos com qual de suas lunetas Galileu fez essas observações, mas podemos deduzir. Comparando esse desenho de Galileu com os catálogos atuais de brilho de estrelas, nota-se que ele enxergou estrelas de até magnitude 9 através da luneta. Ou seja, sua luneta permitia um ganho de três magnitudes. Como o ganho em magnitudes = 2,5 x logaritmo do ganho em luminosidade, isso significa que a objetiva da luneta coletou 16 vezes mais luz que o olho nu, o que dá um diâmetro quatro vezes maior que o da pupila. Como a pupila à noite tem ~0,6 cm de abertura, deduz-se que a objetiva da luneta de Galileu tinha 2,5 cm de diâmetro. De fato, esse era o diâmetro das primeiras lunetas galileanas.

Seguindo esse mesmo raciocínio, não é difícil mostrar que se Galileu tivesse um telescópio como o SOAR, cujo espelho primário tem 4,1 metros de diâmetro, conseguiria observar astros 467 mil vezes mais fracos que a olho nu (ganho de 14 magnitudes), o que implica um limite de magnitude 20. Através do SOAR, se poderia enxergar uma estrela como o Sol a 37 mil anos-luz, enquanto a olho nu o limite de visibilidade do Sol seria de apenas 65 anos-luz (1 ano-luz = 9.460.536.207.068.016 metros; ou também 63.241,07710 unidades astronômicas – UA). Esses cálculos mostram por que o poder coletor, ou seja, o diâmetro da objetiva é o parâmetro mais importante de um telescópio/luneta, e isso é bem exemplificado por uma imagem moderna das Plêiades, que mostra que esse aglomerado contém mais de uma centena de estrelas, em vez das apenas 35 vistas por Galileu. O poder coletor permite revelar astros de brilho mais fraco que o limite detectado pelo olho humano.

O segundo parâmetro de uma luneta/telescópio é o poder resolvente, homólogo à acuidade na visão humana. Quanto menor as coisas que se enxerga, maior o poder resolvente. Desenhe dois pontinhos bem próximos entre si numa folha de papel. Pregue-a na parede e se afaste até não conseguir mais distinguir um do outro. A esta distância, a separação angular entre eles é de 2 minutos de arco, se você tiver uma acuidade visual típica. Conhecimentos elementares de geometria permitem calcular o poder resolvente de seu olho usando um triângulo tendo como base os dois pontos na folha e sua distância até a parede. Com esse poder resolvente conseguimos distinguir uma pessoa a uma distância de ~3,5 km (separar um ponto localizado na cabeça de outro nos pés). As primeiras lunetas de Galileu permitiam um fator quatro vezes maior, ou seja 15 km. Foi isso que encantou seus patrocinadores. Eles podiam avaliar quantos soldados e quantas armas havia no convés dos navios inimigos muito antes que entrassem no porto.

Limite do olho

O poder resolvente de uma lente cresce proporcionalmente ao seu diâmetro. Para a luz visível, uma objetiva de 10 cm tem poder resolvente de 1 segundo de arco (1”), o que é ~120 vezes melhor que a vista desarmada. Com uma lunetinha menor que essa, Galileu revelou as crateras e as montanhas da Lua, as fases do planeta Vênus, as manchas solares, as luas de Júpiter etc. O poder resolvente permite ver coisas menores que o limite do olho humano.

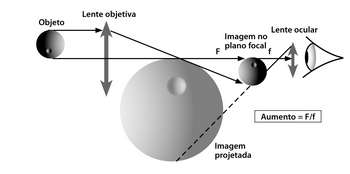
A objetiva projeta a imagem em um plano focal, a uma certa distância (distância focal). Se colocarmos o olho no plano focal da objetiva, o brilho da imagem do astro será maior que a olho nu, mas não necessariamente enxergaremos mais detalhes. Isso porque a imagem no plano focal é, em geral, muito pequena e precisamos ampliá-la para enxergar os detalhes. Para isso, usa-se uma segunda lente, de menor distância focal que a objetiva, a chamada ocular. O fator de ampliação (ou aumento) da ocular é determinado pela razão entre a distância focal da objetiva da ocular. Assim, uma ocular de 10 cm de distância focal, acoplada a uma objetiva de 1 metro de distância focal permite aumento de 10 vezes. Outra, de 1 cm dá aumento de 100 vezes. Jogando com esses dois números é possível obter fatores de aumento de até milhares de vezes. Esse fator não tem a menor importância para os astrônomos profissionais, desde que passaram a coletar as imagens sobre detectores e só depois, durante o dia, se dão ao trabalho de ampliá-las.

O “aumento” é um número que os vendedores geralmente usam para impressionar os compradores novatos de lunetas. Note que uma ocular com mil vezes de aumento é imprestável para a observação com lunetas. Entre os diversos motivos está o fato de que a atmosfera deforma as imagens dos astros, transformando estrelas puntiformes em pequenos borrões de alguns segundos de arco. De nada adianta ter o poder resolvente da óptica de um telescópio maior se o fator limitante é a atmosfera. Por isso, embora os telescópios tenham aumentado surpreendentemente em poder coletor desde a luneta de Galileu, a nitidez das imagens não melhorou muito nesses 400 anos, pois esteve limitada pela atmosfera terrestre e não pela óptica do telescópio. Só recentemente a tecnologia vem conseguindo superar o limite atmosférico.

Fonte: Astronomy Brasil